Sendo considerado um dos conceitos mais primitivos da Matemática, conjuntos não possuem uma definição específica, porém são extremamente utilizados nos ramos da Matemática.
BÁSICO
Representa-se conjuntos (na forma tabular) da seguinte forma:
A = {a, b, c}
Um conjunto sempre deve estar entre chaves. A representa o conjunto, e os termos a, b e c separados por vírgulas correspondem aos elementos do conjunto A (a ∈ A, lê-se "a é elemento de A"). Para separar um elemento e outro devem ser usadas vírgulas.
Também podemos representar o conjunto por uma propriedade:
A = {x | x tem a propriedade p}
Lê-se "A é o conjunto de todos os elementos x tal que x tem a propriedade p". Exemplo:
V = {x | x é uma vogal} -> Nesse caso, sabemos que V = {a, e, i, o, u}
I = {x | x é um número ímpar} -> Nesse caso I = {... −5, −3, −1, 1, 3, 5...}
Usamos os exemplos acima para ir ao próximo conceito:
V = {a, e, i, o, u} -> O conjunto é considerado finito, pois se contarmos todos os elementos do conjunto, chegaremos ao seu fim.
I = {... −5, −3, −1, 1, 3, 5...} -> Nesse caso, o conjunto é considerado infinito, pois não importa o quanto contarmos, sempre haverão elementos para se contar neste tipo de conjunto.
No caso do conjunto A = {x | x é um número primo divisível por 2}, A é um conjunto unitário, pois só há um elemento neste conjunto, que no caso é A = {2}.
Já no conjunto B = {x | x é um número par não divisível por 2}, temos um conjunto vazio (representado por B = ∅), pois segundo a regra, todo número par é divisível por 2.
Subconjuntos
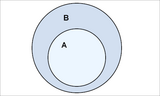
Considere o conjunto M formado por pacientes especiais, que estão com alto risco de morte, e outro conjunto P formado por todos os pacientes de determinado hospital. Nesse caso, dizemos que M é subconjunto de P (M ⊂ P), pois todos os pacientes especiais também fazem parte do conjunto dos pacientes do hospital.
A definição de subconjunto é: "Se A é subconjunto de B, então todo elemento de A é elemento de B". De forma fácil de entender, se o número 1 está no conjunto A, e este é subconjunto de B, logicamente o número 1 também será um elemento do conjunto B. Lê-se "A está contido em B".
Veremos agora as propriedades dos subconjuntos, sendo elas:
- Vazio (∅) é subconjunto de qualquer conjunto, qualquer que seja ele (∅ ⊂ A, ∀ A);
- Todo conjunto é subconjunto dele mesmo, qualquer que seja ele (A ⊂ A, ∀ A);
- Se A é subconjunto de B, e B é subconjunto de A, então os dois conjuntos são equivalentes (A ⊂ B, B ⊂ A ⇒ A = B);
- Se A é subconjunto de B, e B é subconjunto de C, então todo elemento de A é elemento de C (A ⊂ B ⊂ C, A ⊂ C)
Conjunto das partes
Sendo n o número de elementos de determinado conjunto A, podemos dizer que os elementos do conjunto das partes de A são todos os subconjuntos de A.
P(A) = {{subconjunto1},{subconjunto2}...}
Afirmando que A = {1, 2, 3}, vamos descobrir P(A):
Subconjuntos: {1} , {1, 2} , {1, 2, 3} , {2, 3} , {2} , {3} , {1, 3} , ∅
P(A) = {{1}, {2}, {3}, {1, 2}, {1, 2, 3}, {2, 3}, {1, 3}, ∅} => 8 elementos
Perceba que P(A) sempre será uma potência de 2, então podemos chegar na seguinte fórmula:
Nº de subconjuntos de A ou de elementos de P(A) = 2 elevado a n
Exemplos:
I) A = {1.83, 1.80, 1.82, 1.90, 1.87, 1.79, 1.89, 1.94, 1.84}, sendo A as alturas dos jogadores de um time de basquetebol. Sabendo disso, defina o número de elementos de P(A).
Contamos no total 9 elementos. Seria bastante trabalhoso contar todos os subconjuntos, por isso, vamos utilizar a fórmula. 2^9 = 512, então há no total 512 subconjuntos de A.
II) Defina a quantidade de elementos no conjunto das partes de V = {
∅}.
De acordo com o senso comum, como não existe nenhum elemento em V, logo P(V) também será ∅. Porém, deve-se ter muito cuidado nessa hora. Devemos lembrar da propriedade do subconjunto: ∅ é subconjunto de todo conjunto.
Seguindo por esse raciocínio, como P(V) são todos os subconjuntos de V, logo ∅ será um elemento de P(V), e um subconjunto de V. Também poderíamos provar o ponto utilizando a fórmula. Como não há nenhum elemento, temos 2^0 = 1 elemento.
OPERAÇÕES COM CONJUNTOS
Intersecção de conjuntos
Como podemos ver na imagem a seguir, A ∩ B (Lê-se "A intersecção B") é o conjunto dos elementos que estão simultaneamente em A e em B.
Exemplos:
I) Sendo A = {1, 2, 3} e B = {3, 4, 5}, defina a intersecção entre os dois conjuntos.
Ao analisarmos o conjunto, vemos que o único número que se repete nos dois conjuntos é o número 3, então A ∩ B = {3}
II) Sendo P = {2, 4, 6} e I = {1, 3, 5}, defina P ∩ I
Como não há valor que esteja simultaneamente em P e I, dizemos que os eles são disjuntos entre si.
Em imagem, o conjunto P estará totalmente fora do conjunto I.
III) Sendo N = {0, 1, 2, 3, 4} e Z = {−4, −3, −2, −1, 0, 1, 2, 3, 4}, defina N ∩ Z.
Ao analisar os conjuntos, podemos observar que todos os elementos de N estão em Z, logo podemos concluir que N ⊂ Z, e, em seguida: Se N ⊂ Z ⇒ N ∩ Z = N.
Logo, N ∩ Z = {0, 1, 2, 3, 4}.
Em imagem, N está totalmente dentro de Z.
União de conjuntos
Define-se A ∪ B como a união de A com B. Basicamente, é a junção de todos os elementos de A com todos os elementos de B.
Exemplos:
I) Sendo A = {5, 4} e B = {3, 2, 1}, defina A ∪ B.
A ∪ B = {5, 4, 3, 2, 1}
II) Sendo C = {2, 3, 4, 6} e D = {1, 2, 5, 6}, defina C ∪ D.
C ∪ D = {1, 2, 3, 4, 5, 6}
Diferença ou complemento
Suponhamos dois conjuntos A e B. A diferença de A para B seria todos os elementos de A que não existem em B. De forma matemática: A − B = {x | x ∈ A e x ∉ B}
Exemplos:
I) Definindo A = {5, 4, 3} e B = {3, 2, 1}, qual o conjunto A − B e B − A?
A − B = {5, 4}, B − A = {2, 1}
II) Definindo X = {7, 9, 2} e Y = {1, 5, 4}, defina X − Y.
X − Y = {7, 9, 2}
III) Sendo C = {1, 2, 3} e D = {1, 2, 3, 4}, qual conjunto se formará de C − D?
C − D = ∅
Em casos de subconjuntividade, ou B ⊂ A (B está contido em A), podemos definir como A − B o conjunto complementar de B em relação a A.
Exemplo:
Sabendo que A = {4, 5, 6} e B = {1, 2, 3, 4, 5, 6} e que A ⊂ B, defina o complemento de A em relação a B.
A − B = {1, 2, 3}
Dúvidas, reclamações ou elogios basta comentar!
É isso, espero que tenham gostado e até mais. :)