Relações métricas no triângulo retângulo

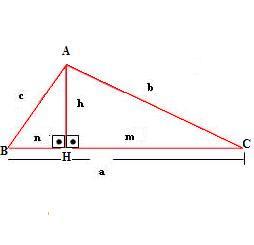
“a” é a hipotenusa. “b” e “c” são os catetos.

   O triângulo retângulo é a base da Trigonometria. Para descobrir seus lados há o método das relações trigonométricas. Porém, quando não se sabe os ângulos opostos aos catetos é necessário utilizar o método das relações métricas. Esse método consiste em utilizar da semelhança de triângulos para obtenção dessas relações.

Relações métricas

   Observe o triângulo acima. Ao traçar a altura h no triângulo ΔABC, surgem os triângulos ΔABH e ΔACH. É necessário fazer a semelhança dos lados entre cada triângulo. Relacione hipotenusa com hipotenusa, o cateto menor com o cateto menor e o cateto maior com o cateto maior.

1º caso: ΔABC ~ ΔABH

a/c = b/h = c/n

ah = bc

bn = hc

c² = an

2º caso: ΔABC ~ ΔACH

a/b = b/m = c/h

b² = am

bh = mc

ah = bc

3º caso: ΔABH ~ ΔACH

c/b = n/h = h/m

bn = hc

h² = mn

bh = mc

4º caso: adicionais.

a² = b² + c²

a = m + n

   As fórmulas riscadas já foram repetidas anteriormente. Não é necessário memorizar as fórmulas, e sim fazer as relações manualmente, Fica muito mais fácil e você não precisa se preocupar em esquecer alguma delas.