Matrizes

MATRIZES

São tabelas que tem o objetivo de agrupar dados, que podem ser números ou até mesmo funções. Quando diz que uma matriz é 2 x 3 quer dizer que ela possui duas linhas e três colunas. (Em outras palavras o primeiro número sempre é a linha o segundo é a coluna). Observe o exemplo abaixo:

Cada número representado dentro do colchete, da figura acima é chamado de "elemento da matriz".

TIPOS DE MATRIZES

Quadrada: É chamada de quadrada, quando a mesma quantidade número de linhas é igual ao de colunas.

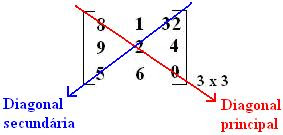
O exemplo acima mostra uma matriz de ordem 3 (3 linhas x 3 colunas). Assim por diante, como a de ordem 4 ( 4 x 4) etc. Observação: diagonal principal x diagonal secundária.

Quando pedir por exemplo os números da diagonal principal: É 8, 2 e o 0. Já o da diagonal secundária: É 32, 2 e o 5. 

Nula: Todos os elementos são zero.

Observe que tanto na linha como na coluna todos são elementos são iguais a zero.

Identidade: Todos os elementos são zero, com exceção que na diagonal principal os números são um.

Genérica: Cada número ocupa seu determinado local definido por sua linha e coluna.

É a partir da genérica que você pode construir as outras matrizes. Exemplo se uma questão pedir que você construa uma matriz 2 x 2 você pega todos os elementos que tiver dentro da 2 x 2 e monta.

Triangular: Acima ou abaixo da diagonal principal é zero. Caso seja ambos, a matriz é diagonal.

Transposta: Consiste na troca entre linha e coluna (Em outras palavras o que é linha vira coluna, e o que é coluna vira linha.

Simétrica: Quando ocorre a troca na transposta de (linha e coluna) essa troca é a simétrica. Em outras palavras, mesmo com essa modificação, a matriz não perde seu valor original, continua sendo a mesma da original.