O cálculo de áreas é importantíssimo para a construção civil.
Primeiras palavras
A seguir, aprenderemos a como calcular a área das diversas figuras planas existentes. O conteúdo será essencial não só para resolver exercícios, provas e vestibulares, mas também para o cotiiano, onde nos deparamos com diversas situações em que há a necessidade de se calcular áreas de diferentes formatos. Vamos prosseguir!
Área de triângulos
Será demonstrada três maneiras básicas de se calcular a área de um triângulo: através da fórmula usual, pela Fórmula dos Lados e pelo Teorema de Heron. Confira a fórmula usual.
Já na Fórmula dos Lados, devemos multiplicar os lados adjacentes pelo seno do ângulo formado e dividir por 2, da seguinte forma.
Pelo Teorema de Heron, devemos saber os lados do triângulo. Sabendo disso, descobriremos o perímetro e, com essa informação, dividiremos por 2 para obter o semiperímetro. Sabendo disso, basta aplicar a seguinte fórmula.
Área de quadriláteros
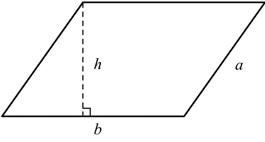
Para calcular a área do retângulo é preciso multiplicar sua base pela sua altura. A fórmula é a mesma para o paralelogramo.
Já para calcular a área do trapézio, devemos somar a base menor com a base maior, multiplicar pela altura e dividir por 2, da seguinte maneira.
Finalizando os quadriláteros, para calcular a área do losango deve-se multiplicar a diagonal maior com a diagonal menor e dividir por 2, desse jeito.
Área da circunferência
Para calcular a área da circunferência devemos saber qual o raio dessa circunferência e em seguida utilizar a fórmula expressa a seguir.
Áreas diversas
Para finalizar, aprenderemos a como calcular a área de um polígono regular. Para demonstrar a fórmula, será utilizado um hexágono. Observe.
Para descobrir h (apótema), basta fazer o Teorema de Pitágoras em um dos triângulos, já que o hexágono foi dividido em seis triângulos equiláteros.
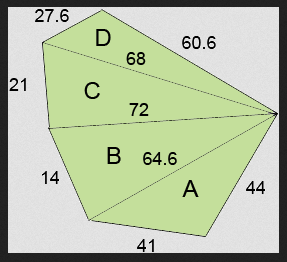
Caso queira calcular a área de um polígono irregular, deverá dividi-la em vários triângulos, descobrir a área de todos eles e em seguida somar as mesmas. Irei resolver um exemplo utilizando o Teorema de Heron.
Começaremos pelo triângulo A. Sabendo que seu perímetro é 159.6, quer dizer que seu semiperímetro é 74.8, basta resolvermos usando a fórmula. Considere a medida dos lados em cm, portanto a área será em cm².
Depois do trabalho imenso, ainda faltam os triângulos B, C e D. Utilizando as mesmas fórmulas, obteremos os seguintes resultados.
Finalmente, a área desse hexágono irregular é de 2843,25 cm².
Obrigado pela sua visita, continue antenado aqui no Prático & Básico.














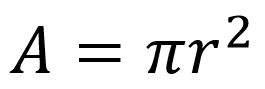

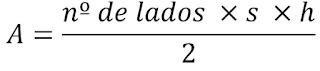










Nenhum comentário:
Postar um comentário